Probability density function

In probability theory, a probability density function (abbreviated as pdf, or just density) of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point in the observation space. The probability of a random variable falling within a given set is given by the integral of its density over the set.
The terms “probability distribution function”[1] and "probability function"[2] have also been used to denote the probability density function. However, special care should be taken around this usage since it is not standard among probabilists and statisticians. In other sources, “probability distribution function” may be used when the probability distribution is defined as a function over general sets of values, or it may refer to the cumulative distribution function, or it may be a probability mass function rather than the density.
Continuous univariate distributions
A probability density function is most commonly associated with continuous univariate distributions. A random variable X has density ƒ, where ƒ is a non-negative Lebesgue-integrable function, if:
Hence, if F is the cumulative distribution function of X, then:
and (if ƒ is continuous at x)
Intuitively, one can think of ƒ(x) dx as being the probability of X falling within the infinitesimal interval [x, x + dx].
Formal definition
This definition may be extended to any probability distribution using the measure-theoretic definition of probability. A random variable X has probability distribution X*P: the density of X with respect to a reference measure μ is the Radon–Nikodym derivative:
That is, ƒ is any function with the property that:
for any measurable set A.
Discussion
In the continuous univariate case above, the reference measure is the Lebesgue measure. The probability mass function of a discrete random variable is the density with respect to the counting measure over the sample space (usually the set of integers, or some subset thereof).
Note that it is not possible to define a density with reference to an arbitrary measure (i.e. one can't choose the counting measure as a reference for a continuous random variable). Furthermore, when it does exist, the density is almost everywhere unique.
Further details
For example, the continuous uniform distribution on the interval [0, 1] has probability density ƒ(x) = 1 for 0 ≤ x ≤ 1 and ƒ(x) = 0 elsewhere.
The standard normal distribution has probability density
If a random variable X is given and its distribution admits a probability density function ƒ, then the expected value of X (if it exists) can be calculated as
Not every probability distribution has a density function: the distributions of discrete random variables do not; nor does the Cantor distribution, even though it has no discrete component, i.e., does not assign positive probability to any individual point.
A distribution has a density function if and only if its cumulative distribution function F(x) is absolutely continuous. In this case: F is almost everywhere differentiable, and its derivative can be used as probability density:
If a probability distribution admits a density, then the probability of every one-point set {a} is given by the probability distribution.
Two probability densities ƒ and g represent the same probability distribution precisely if they differ only on a set of Lebesgue measure zero.
In the field of statistical physics, a non-formal reformulation of the relation above between the derivative of the cumulative distribution function and the probability density function is generally used as the definition of the probability density function. This alternate definition is the following:
If dt is an infinitely small number, the probability that X is included within the interval (t, t + dt) is equal to ƒ(t) dt, or:
Link between discrete and continuous distributions
The definition of a probability density function at the start of this page makes it possible to describe the variable associated with a continuous distribution using a set of binary discrete variables associated with the intervals [a; b] (for example, a variable being worth 1 if X is in [a; b], and 0 if not).
It is also possible to represent certain discrete random variables as well as random variables involving both a continuous and a discrete part with a generalized probability density function, by using the Dirac delta function. For example, let us consider a binary discrete random variable taking −1 or 1 for values, with probability ½ each.
The density of probability associated with this variable is:
More generally, if a discrete variable can take n different values among real numbers, then the associated probability density function is:
where  are the discrete values accessible to the variable and
are the discrete values accessible to the variable and  are the probabilities associated with these values.
are the probabilities associated with these values.
This substantially unifies the treatment of discrete and continuous probability distributions. For instance, the above expression allows for determining statistical characteristics of such a discrete variable (such as its mean, its variance and its kurtosis), starting from the formulas given for a continuous distribution.
Probability functions associated with multiple variables
For continuous random variables  , it is also possible to define a probability density function associated to the set as a whole, often called joint probability density function. This density function is defined as a function of the n variables, such that, for any domain D in the n-dimensional space of the values of the variables
, it is also possible to define a probability density function associated to the set as a whole, often called joint probability density function. This density function is defined as a function of the n variables, such that, for any domain D in the n-dimensional space of the values of the variables  , the probability that a realisation of the set variables falls inside the domain D is
, the probability that a realisation of the set variables falls inside the domain D is
If F(x1, …, xn) = Pr(X1 ≤ x1, …, Xn ≤ xn) is the cumulative distribution function of the vector (X1, …, Xn), then the joint probability density function can be computed as a partial derivative
Marginal densities
For i=1, 2, …,n, let  be the probability density function associated to variable
be the probability density function associated to variable 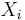 alone. This is called the “marginal” density function, and can be deduced from the probability densities associated of the random variables
alone. This is called the “marginal” density function, and can be deduced from the probability densities associated of the random variables  by integrating on all values of the n − 1 other variables:
by integrating on all values of the n − 1 other variables:
Independence
Continuous random variables  are all independent from each other if and only if
are all independent from each other if and only if
Corollary
If the joint probability density function of a vector of n random variables can be factored into a product of n functions of one variable
then the n variables in the set are all independent from each other, and the marginal probability density function of each of them is given by
Example
This elementary example illustrates the above definition of multidimensional probability density functions in the simple case of a function of a set of two variables. Let us call  a 2-dimensional random vector of coordinates
a 2-dimensional random vector of coordinates  : the probability to obtain
: the probability to obtain  in the quarter plane of positive x and y is
in the quarter plane of positive x and y is
Sums of independent random variables
The probability density function of the sum of two independent random variables U and V, each of which has a probability density function, is the convolution of their separate density functions:
It is possible to generalize the previous relation to a sum of N independent random variables, with densities  :
:
Dependent variables and change of variables
If the probability density function of an independent random variable  is given as
is given as  , it is possible (but often not necessary; see below) to calculate the probability density function of some variable
, it is possible (but often not necessary; see below) to calculate the probability density function of some variable 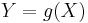 . This is also called a “change of variable” and is in practice used to generate a random variable of arbitrary shape
. This is also called a “change of variable” and is in practice used to generate a random variable of arbitrary shape 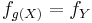 using a known (for instance uniform) random number generator.
using a known (for instance uniform) random number generator.
If the function g is monotonic, then the resulting density function is
Here 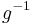 denotes the inverse function and g' denotes the derivative.
denotes the inverse function and g' denotes the derivative.
This follows from the fact that the probability contained in a differential area must be invariant under change of variables. That is,
or
For functions which are not monotonic the probability density function for y is
where 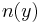 is the number of solutions in x for the equation
is the number of solutions in x for the equation  , and
, and 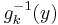 are these solutions.
are these solutions.
It is tempting to think that in order to find the expected value  one must first find the probability density
one must first find the probability density 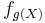 of the new random variable
of the new random variable 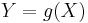 . However, rather than computing
. However, rather than computing
one may find instead
The values of the two integrals are the same in all cases in which both  and
and 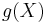 actually have probability density functions. It is not necessary that g be a one-to-one function. In some cases the latter integral is computed much more easily than the former.
actually have probability density functions. It is not necessary that g be a one-to-one function. In some cases the latter integral is computed much more easily than the former.
Multiple variables
The above formulas can be generalized to variables (which we will again call y) depending on more than one other variable.  shall denote the probability density function of the variables y depends on, and the dependence shall be
shall denote the probability density function of the variables y depends on, and the dependence shall be  . Then, the resulting density function is
. Then, the resulting density function is
where the integral is over the entire (m-1)-dimensional solution of the subscripted equation and the symbolic dV must be replaced by a parametrization of this solution for a particular calculation; the variables  are then of course functions of this parametrization.
are then of course functions of this parametrization.
This derives from the following, perhaps more intuitive representation: Suppose x is an n-dimensional random variable with joint density f. If 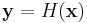 , where H is a bijective, differentiable function, then y has density g:
, where H is a bijective, differentiable function, then y has density g:
with the differential regarded as the Jacobian of the inverse of H, evaluated at y.
Finding moments and variance
In particular, the nth moment 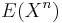 of the probability distribution of a random variable X is given by
of the probability distribution of a random variable X is given by
and the variance is
or
See also
- Likelihood function
- Density estimation
- Secondary measure
- Probability mass function
References
- Ushakov, N.G. (2001), "Density of a probability distribution", in Hazewinkel, Michiel, Encyclopaedia of Mathematics, Springer, ISBN 978-1556080104, http://eom.springer.de/D/d031110.htm
Bibliography
- Pierre Simon de Laplace (1812). Analytical Theory of Probability.
-
- The first major treatise blending calculus with probability theory, originally in French: Théorie Analytique des Probabilités.
- Andrei Nikolajevich Kolmogorov (1950). Foundations of the Theory of Probability.
-
- The modern measure-theoretic foundation of probability theory; the original German version (Grundbegriffe der Wahrscheinlichkeitrechnung) appeared in 1933.
- Patrick Billingsley (1979). Probability and Measure. New York, Toronto, London: John Wiley and Sons.
- David Stirzaker (2003). Elementary Probability.
-
- Chapters 7 to 9 are about continuous variables. This book is filled with theory and mathematical proofs.
External links
- Weisstein, Eric W., "Probability density function" from MathWorld.
|
|||||||||||||
![\operatorname P [a \leq X \leq b] = \int_a^b f(x) \, \mathrm{d}x .](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/f5594414fcb5938e0d2f91545a851e18.png)
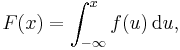

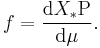
![\mathrm P [X \in A ] = \int_{X^{-1}A} \, \mathrm d \operatorname{P} = \int_A f \, \mathrm d \mu](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/c218199850f669d61b9028702ee79761.png)
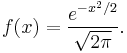




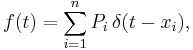
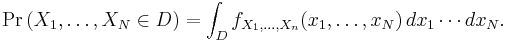


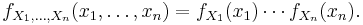

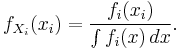


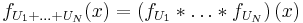

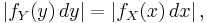

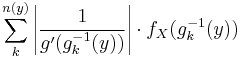
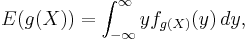

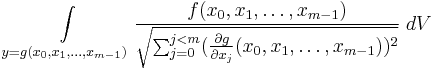
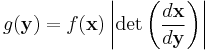

![\operatorname{var}(X) = E[(X - E(X))^2] = \int_{-\infty}^\infty (x-E(X))^2 f_X(x)\,dx](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/66eaf594b660c6f8641c7a911b446444.png)
![\operatorname{var}(X) = E(X^2) - [E(X)]^2.\,](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/41bc5a4c74aed8c8ba726aa4cde53b73.png)
